By Lance Coleman. 

This excerpt from Lance Coleman’s new book Advanced Quality Auditing: An Auditor’s Review of Risk Management, Lean Improvement, and Data Analysis examines statistics for auditors.

Often as auditors we need to review statistical data as part of our review of documented information. With that being the case, having a basic understanding of statistical principles is as easy to attain as it is important to master.

A sample is a randomly selected group pulled from a homogenous population for the purpose of making observations about that population as a whole. Sampling is a means of making predictions about a population under study based on the observations made by taking a sample. Sampling may or may not  be statistically valid. Statistically valid sampling as used in business and industry today is often likely to come from a normal or bell-shaped distribution.

Normal  distribution: Much of the data that we review and analyze relating to our processes has a population that falls into a normal distribution pattern. The nature of this pattern allows for predictive modeling, which we use in design of experiments for validation and optimization of processes and when determining if a process is capable and/or in control. The two most important aspects of a process output are location (where centered) and dispersion (how spread out).

There are three measurements of a population center:

• Mean – (also known as the average) is the total of all values divided by the total number of values; mathematically it is referred to as x-bar
• Median –  the middle value in the range of values; if there are an even number of values, then the center of the middle two values is selected as the median (i.e., if the middle two values of a set of numbers are 70 and 71, then the median would be 70.5)
• Mode – the most frequently occurring value in a data set

Note:  Although there will always be both a mean and a median associated with a set of numbers, there does not have to be a mode.

There are three measures of dispersion (how spread out) of a population:

• Range – the largest value minus the smallest value in a population
• Standard deviation – can be thought of the “average” distance between each data point in a population. The equation for standard deviation (also called sigma – σ)  is σ = SQRT{Σ(x_n– xbar)²/(n-1)} where “n” is the number of samples chosen
• Variance – the square of the standard deviation; this is significant for designed experiments because variance can be added and subtracted.

 

In a normal distribution, standard deviation allows us to determine where a specific percentage of the population is located, which allows us to make predictions on future behavior:

• 68.2% of a normal population is within +/- 1 σ  of the population mean
• 95.4% of a normal population is within +/- 2 σ of the population mean
• 99.7% of a population is within +/- 3 σ  of the population mean

 

As there are no perfect processes, all processes have some amount of variation from cycle to cycle or unit to unit. The types of variation found in a normal distribution are common cause and special cause variation:

• Common cause: Variation that is normal to the process. Attempts to adjust a process for normal cause variation often makes things worse.
• Special cause: Variation outside or within the three sigma control limits caused by an external factor. Root cause should be determined and corrective action applied to eliminate special cause variation

Control Charts

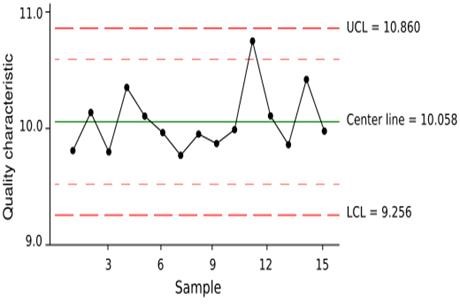
Control charts are used to plot data that conforms to a normal (or bell-shaped) distribution pattern. Control charts capture the two most important data for describing a population: the location (where centered) and dispersion (how spread out). Control charts (see figure 1 below) are used to:

• Monitor a process
• Assess process control
• Assess process capability

 

Figure 1 – Sample Control Chart

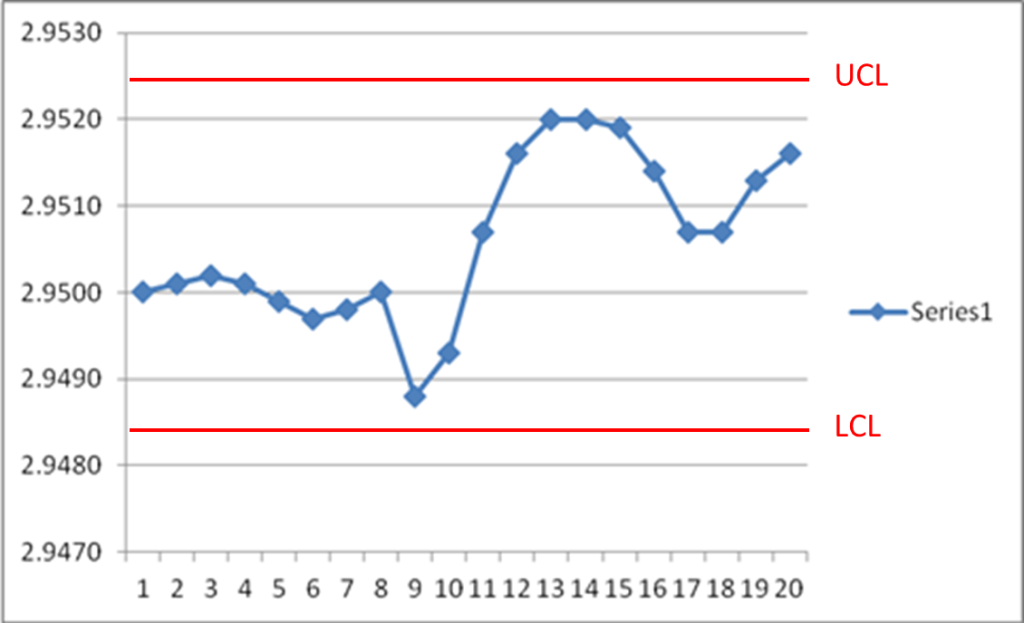
Figure 2 below shows aberrant behavior within the control limits, where a sinusoidal pattern suddenly shifts and greatly increases in variation.

Figure 2 – Control Chart Showing Special Cause Variation

At the start of my career, one of my mentors shared this bit of wisdom: Once is an incident, twice may be coincidence, but three times starts to look like a trend. This advice still rings true whether you are talking about audit evidence that has been collected from the floor or data plotted on a control chart. Three data points or even three out of four, in one direction over time is something that may bear watching or reporting to the process owner. There are many other variables to consider, but as a rule of thumb this scenario at the very least should precipitate a “second look” or review of subsequent data points. Westinghouse, one of the early pioneers in statistical process control (SPC) using control charts, identified certain data patterns that were indicative of negative trends requiring investigation. These later became known as the Westinghouse Rules. A partial listing is below:

• Any single data point that falls outside 3 standard deviations from the process centerline
• Two out of three consecutive points fall between 2 and 3 standard deviations from the process centerline
• Four out of five consecutive points fall between 1 and 3 standard deviations from the process centerline
• Eight consecutive points fall on the same side of the centerline

 

Auditors seeing similar trends in data they are reviewing should inquire as to if the trend was investigated? Under what circumstances would process data cause an investigation to be launched? What do operators/technicians do when they see an out-of-control condition? The auditor should also inquire as to what statistical process control training is provided.

Control chart (knowledge) is a huge opportunity for auditor impact that doesn’t require a substantial statistical knowledge. In the medical device field, it’s a common requirement to report out of specification/tolerance conditions to the area supervisor. So much so that there is a commonly recognized acronym (OOS/OOT). However, you would be surprised how infrequently it is required to report out of control conditions. There are recognized trends of vacillating or drifting process such as, 14 data points alternating up and down, 7 consecutive data points above the mean, or 6 or more data points ascending in value. Similarly, it is even less common to have other unusual trends reported. In addition to reviewing data, the auditor might ask the question, “What do you do when certain trends are noted?” Also, how do you know what to do? Is it through training or through a work instruction or both? By asking these types of questions, potential gaps in the monitoring program may be identified and closed.

While reviewing data during audits I have actually seen a 0.05″ measurement indicated as meeting a 0.050″ maximum requirement. The obvious issue is how do you know the dimension is in spec without knowing the third digit? A measuring device should read at a minimum the same number of decimal places as the parameter under review and preferably one decimal place more.  Besides a possible conformance issue, there is a possible training opportunity or an identified need to improve a piece of equipment with insufficient resolution for the measurement that it is being used to take.

Hopefully, this simple overview will assist you when you review process data during your next audit.

About the author

Lance B. Coleman is the principal consultant for Full Moon Consulting and has more than 20 years of leadership experience in the areas of quality engineering, lean implementation, quality and risk management in the medical device, aerospace, and other regulated industries. He has a degree in electrical engineering technology from the Southern Polytechnical University. He is an American Society for Quality Senior Member, Certified Quality Engineer, Six Sigma Green Belt, Quality Auditor, and Biomedical Auditor. He is an Exemplar Global Principal QMS Auditor.

Coleman is the author of The Customer Driven Organization: Employing the Kano Model (Productivity Press 2014)  and Advanced Quality Auditing: An Auditor’s Review of Risk Management, Lean Improvement and Data Analysis (Quality Press 2015), as well as many articles on risk management, lean, and quality. Coleman is also an instructor for the ASQ Certified Quality Auditor Preparatory Course and the editor of the ASQ Audit Division newsletter. He has presented, trained, and consulted throughout the United States and abroad.

TAG: statistics for auditors.